The Study Of Schumann Resonance In Iowa
- Vert Arbusto
- Sep 15, 2022
- 5 min read
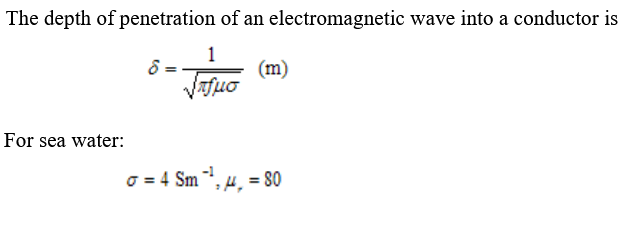
15 Sept 2022. The Study Of Schumann Resonance In Iowa
by Anton Kruger , Sponsor: Iowa Space Grant Consortium
Globally, the terrestrial surface forms a nearly perfect conductor. The sun’s radiation creates the ionosphere at 70–1,500 km altitudes, and the two spherical conductors form an electromagnetic resonant cavity.
Lightning discharges in the cavity create global resonances in the 5–50 Hz range.
By measuring these Schumann Resonances one can infer lighting and thunderstorm activity planetary-wide.
This is important since much of the lighting occurs in inaccessible parts of the world.
Lightning is related to thunderstorms and rainfall, and in turn to global temperatures.
NASA-sponsored researchers have used Schumann Resonance measurements in global- precipitation and warming studies.
There is a handful of Schumann Resonance receivers in Arizona, and the East- and West Coasts, but none in the central U.S.
The Iowa Space Grant Consortium has provided funding to construct a Schumann Resonance receiver and to deploy it in rural Johnson County, Iowa—an ideal location, relatively isolated from man-made electrical noise.
A Schumann Resonance receiver measures very weak electric and magnetic fields in the ultra-low frequency (ULF) and extremely low frequency (ELF) bands, and requires custom electronics and special antennas.
Schumann Resonances
On a global scale, the terrestrial surface is a near-perfect conductor.
Radiation from the sun ionizes the earth’s atmosphere and forms a conducting plasma layer (regions of uniform electron density) at altitudes form 70–1,500 km.
The D-layer, an important factor in Schumann Resonances, is at 70–80 km. If the earth were shrunk to the size of an orange (~ 50 mm), the D-layer would be at 50.3 mm.
In other words, the layers are very close to the surface of the earth. These nominally concentric conductors have long been exploited for long-range radio communications.
Radio waves are reflected off the ionosphere to the terrestrial surface where they are reflected back to the ionosphere and so on. In fact, the earth and ionosphere form an electromagnetic resonant cavity.
[ Fig. 1 ]
The resonant frequency of the cavity falls in the ultra-low frequency (ULF) and extremely low frequency (ELF) bands in the range of 5–50 Hz, and depends on several factors, including the electrical parameters of the atmosphere, and the state (height, ionization level) of the ionosphere.
Under proper conditions a wave can traverse the planet several times before being attenuated below detection levels. Lightning discharges produce electromagnetic waves.
Globally, there are an estimated 100 lightning strikes per second. The current that flows in an average lightning bolt is in the order of 20,000 A.
Since the 1950s it has been known that broadband electrical noise resulting from the lightning discharges inside the earth-ionosphere cavity excite so-called Schumann Resonances (SR), named after their discoverer (Schumann, 1952).
By making a number of reasonable assumptions, one can derive analytical expressions for the resonant frequencies of the earth-ionosphere cavity.
The nominal frequencies are 7.5, 14.5 20, 26 Hz. The amplitude of the resonances decreases with frequency.
[ Fig 2 ]
Measuring Schumann Resonances
SR frequencies are low.
Practical antennas have to be small fractions of the wavelength, and are inefficient.
For example, a ½-wave antenna at 7.5 Hz, one of nominal SR frequencies, would have to be 20,000 km long.
Such low frequencies suffer very low attenuation in the atmosphere and penetrate significant distances underground and into the ocean.
The depth of penetration of an electromagnetic wave into a conductor is:
(See image for equation.)
For sea water:
(See image for equation.)
At 5 MHz the penetration is about 0.12 m. However, at 5 Hz, the penetration is 112 m.
Thus, ELF/ULF electromagnetic waves (5–50 Hz) penetrate deep into earth and ocean, and are used for submarine communications (U.S. 77 Hz, Russia 83 Hz).
The electric (E) field of the SR is much smaller than the static E-field in the atmosphere.
The SR E-field is in the mV/m range, superimposed on earth’s 100 V/m in fair weather to 3 kV/m on a stormy day—four to six orders of magnitude smaller.
The magnetic (B) field of the SR is likewise orders of magnitude (pT range) smaller than the earth’s magnetic field (50,000 nT range). Special receivers and antennas are thus needed to measure the SR.
The E-field is commonly measured with a ball antenna connected to a high-impedance amplifier.
The B-field is measured with a large (~ 1 m) magnetic coil that consists of many (>50,000) turns around a material with very high magnetic permeability.
One popular alloy, MuMetal, can have a relative magnetic permeability of 240,000 and higher. For comparison, pure iron’s relative permeability is ~ 150.
Sample Spectra
The figure below shows a sample spectrum of B-field obtained with the receiver.
Spikes in the spectrum are noise, mostly from unknown sources. This spectrum was obtained with the receiver in the vicinity of power lines.
Despite filtering, the 60 Hz power line frequency is clearly visible. The Schumann Resonances are the broad bumps n the spectrum. They are at 6.5, 18, and 27 Hz in this spectrum.
There is considerable fluctuation in the spectrum over short time periods. This spectrum is for a 5-minute interval.
Interesting patterns manifest when one averages spectra over daily and monthly scales.
[ Fig. 3 ]
The following figure illustrates why one would expect a diurnal effect on the Schumann Resonance.
The sun does not ionize the atmosphere on the dark side of the earth and some of the layers disappear.
These layers begin to form again at sunrise.
The cavity is thus not symmetrical and undergoes a daily modulation by the sun.
[ Fig. 4 ]
Lightning is not evenly distributed over the planet. Most lightning occurs over land, as the figure below shows.
The lightning centers migrate from north to south and back over the course of a year.
There are long-term climate oscillations that affect rainfall and lightning.
All these factors affect the magnitude and frequency of the Schumann Resonance.
[ Fig. 5 ]
Schumann Resonances and Global Temperature
Clearly, the magnitude of the SR is related to the number of lightning strokes (~ 100 per second) occurring worldwide.
It is well known that thunderstorms and lightning strokes in many parts of the world are directly related to lower-atmospheric air temperatures.
Higher temperatures produce more lightning strokes.
Earle Williams (1992) linked Schumann Resonances to convection and tropical and/or global temperature.
He used SR data from receivers from several locations to support his arguments.
There is a debate over the sensitivity of the SR to global temperature, but there is a consensus about the connection. This is important in global climate studies.
References
Kruger, A., and K. Kanukurthy, A cell phone-based data logger and network for monitoring environmental variables. IEEE Transactions on Instrumentation and Measurement, 2004 (In preparation).
Price, C., and D. Rind, 1994, Possible implications of global climate change on global lightning distributions and frequencies. Journal of Geophysical Research, 99, 10,823–10,831.
Schumann, W.O., 1952, Über die strahlungslosen Eigenschwingungen einer leitenden Kugel, die von einer Luftschicht und einer Ionosphärenhülle umgeben ist. Zeitschrift Naturforsch, 7A, 149–154.
Williams, E.R., 1992, The Schumann Resonance: A global tropical thermometer. Science, 256, 1184–1187.
Resonances in the Earth-Ionosphere Cavity, Alexander P. Nickolaenko, Usikov Institute for Radio-Physics and Electronics, National Academy of Sciences of the Ukraine, Kharkov, Ukraine and Masashi Hayakawa, Dept. of Electronic Engineering, The University of Electro-Communications, Tokyo, Japan (Kluwer), 2002.
_
Patreon: ( https://www.patreon.com/posts/72014416?pr=true )
Wordpress: ( https://vertearbustosschumannresonanceharmonics.wordpress.com/2022/09/15/the-study-of-schumann-resonance-in-iowa/ )







Comments